l-state Solutions of the Relativistic and Non-Relativistic Wave Equations for Modified Hylleraas-Hulthen Potential Using the Nikiforov-Uvarov Quantum Formalism
Hitler Louis1* , Ita B. Iserom1 , Ozioma U. Akakuru1 , Nelson A. Nzeata-Ibe1 , Alexander I. Ikeuba1 , Thomas O. Magu1 , Pigweh I. Amos2 and Edet O. Collins3
1Physical/Theoretical Chemistry Unit, Department of Pure and Applied Chemistry, School of Physical Sciences, University of Calabar, Calabar, Cross River State Nigeria .
2Department of Chemistry, School of Physical Sciences, Modibbo Adama University of Technology, Yola, Adamawa State Nigeria .
3Department of Physics, School of Physical Science, Federal University of Technology, Minna, Niger State Nigeria .
Corresponding author Email: louismuzong@gmail.com
DOI: http://dx.doi.org/10.13005/OJPS03.01.02
An exact analytical and approximate solution of the relativistic and non-relativistic wave equations for central potentials has attracted enormous interest in recent years. By using the basic Nikiforov-Uvarov quantum mechanical concepts and formalism, the energy eigenvalue equations and the corresponding wave functions of the Klein–Gordon and Schrodinger equations with the interaction of Modified Hylleraas-Hulthen Potentials (MHHP) were obtained using the conventional Pekeris-type approximation scheme to the orbital centrifugal term. The corresponding unnormalized eigen functions are evaluated in terms of Jacobi polynomials.
Copy the following to cite this article:
Louis H, Iserom I. B, Akakuru O. U, Nzeata-Ibe N. A, Ikeuba A. I, Magu T. O, Amos P. I, Collins E. O. l-state Solutions of the Relativistic and Non-Relativistic Wave Equations for Modified Hylleraas-Hulthen Potential Using the Nikiforov-Uvarov Quantum Formalism. Orient J Phys Sciences 2018;3(1).
DOI:http://dx.doi.org/10.13005/OJPS03.01.02Copy the following to cite this URL:
Louis H, Iserom I. B, Akakuru O. U, Nzeata-Ibe N. A, Ikeuba A. I, Magu T. O, Amos P. I, Collins E. O. l-state Solutions of the Relativistic and Non-Relativistic Wave Equations for Modified Hylleraas-Hulthen Potential Using the Nikiforov-Uvarov Quantum Formalism. Orient J Phys Sciences 2018;3(1). Available from: https://bit.ly/3ruHnFM
Download article (pdf) Citation Manager
Select type of program for download
| Endnote EndNote format (Mac & Win) | |
| Reference Manager Ris format (Win only) | |
| Procite Ris format (Win only) | |
| Medlars Format | |
| RefWorks Format RefWorks format (Mac & Win) | |
| BibTex Format BibTex format (Mac & Win) |
Introduction
Quantum mechanical Wavefunctions and their corresponding eigenvalues give significant information in describing various quantum systems.1,3 Bound state solutions of relativistic and nonrelativistic wave equation arouse a lot of interest for decades. Schrodinger wave equations constitute nonrelativistic wave equation while Klein-Gordon and Dirac equations constitute the relativistic wave equations.1,5 The quantum mechanical interacting potentials (MHHP) can be used to compute and predict the bound state energies for both homonuclear and heteronuclear diatomic molecules. Other potentials that have been used to investigate bound state solutions are as follows: Coulomb, Poschl-Teller, Yukawa, Hulthen, Hylleraas, pseudoharmonic, Eckart and many other potential combinations.6,13 The aforementioned potentials are studied with some specific quantum mechanical methods and concepts like the following: Wentzel, Kramers, and Brillouin known as the WKB approximation, asymptotic iteration method, Nikiforov-Uvarov method, formular method, supersymmetric quantum mechanics approach, exact quantization, and many more.14,24
In theoretical physics, the shape form of a potential plays a significant role, particularly when investigating the structure and nature of the interaction between systems. Therefore, our aim, in this present work, is to investigate approximate bound state solutions of the Klein-Gordon and Schrodinger equations with newly proposed Modified Hylleraas-Hulthen potential (MHHP) using the conventional parametric Nikiforov-Uvarov (NU) method. The solutions of this equation will definitely give us a wider and deeper knowledge of the properties of molecules moving under the influence of the mixed interacting potentials which is the goal of this paper. The parametric NU method is very convenient and does not require the truncation of a series like the series solution method which is more difficult to useThis article is divided into five sections. Section 1 is the introduction; Section 2 is the brief introduction of Nikiforov-Uvarov quantum mechanical concept. In Section 3, we presented the angular solutions to Klein-Gordon and Schrodinger wave equations using the proposed potential and obtained both the energy eigenvalue and their corresponding normalized. We gave a brief discussion and conclusion in sections 4 and 5 respectively
Theory of Parametric Nikiforov-Uvarov Method
The parametric form is simply using parameters to obtain explicitly energy eigenvalues and it is still based on the solutions of a generalized second order linear differential equation with special orthogonal functions. The NU is based on solving the second order linear differential equation by reducing to a generalized equation of hyper-geometric type. This method has been used to solve the Schrödinger, Klein–Gordon and Dirac equation for different kind of potentials.24,31 The second-order differential equation of the NU method has the form.
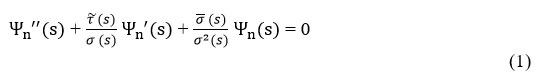
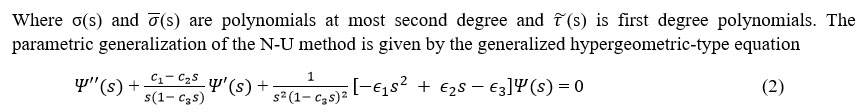
Thus eqn. (2) can be solved by comparing it with equation (3) and the following polynomials are obtained
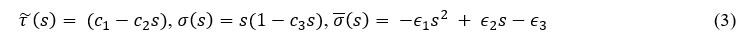
The parameters obtainable from equation (4) serve as important tools to finding the energy eigenvalue and eigenfunctions. They satisfy the following sets of equation respectively
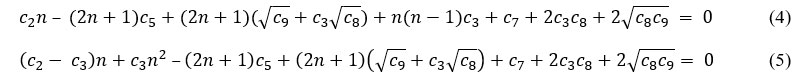
While the wave function is given as
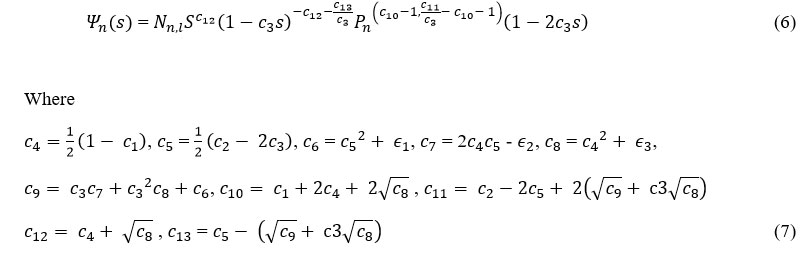
and Pn is the orthogonal polynomials.
Solutions of the wave equations
Solutions of the Klein-Gordon equation
The Klein-Gordon Equation [29] with vector V(r), potential in atomic units (ħ = c = 1) is given as
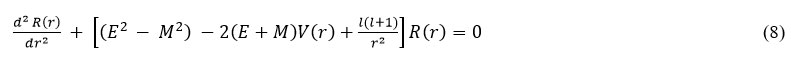
Where E, M, I and V (r) are the Energy, reduced mass, angular momentum and potential
The Modified Hylleraas Potential
The Modified Hylleras Potential as proposed by ref.32 is given as:

where a and b are Hylleraas potential screening parameters while Vo is the potential depth and S is the transformation, thus

Eqn. (9b) is the relationship between S and r, the so-called transformation!
The Hulthen Potential
The Hulthen potential is one of the important short-range potentials, which behaves like a Coulomb potential for small values of r and decreases exponentially for large values of r. 33 The Hulthen potential in it simplest form is given as:

Where Vo and S are the potential depth and the transformation parameter respectively.
The Modified Hylleraas-Hulthen Potential
The Modified Hylleraas-Hulthen potential is our newly proposed interacting potential which is formed by combining eqns. (9) and (10) to get eqn. (11) given as:

Where all the parameters have their usual meaning
Substitute eqn. (11) into eqn. (8) gives:
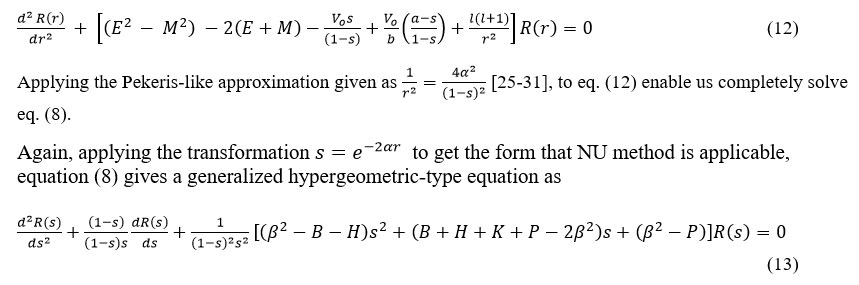
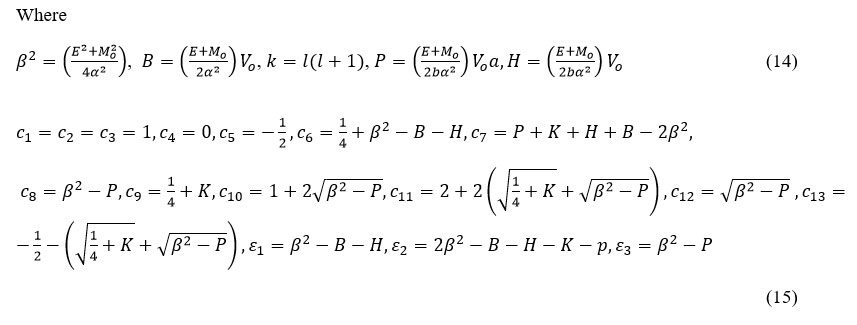
Now using equations (6), (14) and (15) we obtain the energyeigen spectrum of the newly proposed interacting potential (MHHP) given as:
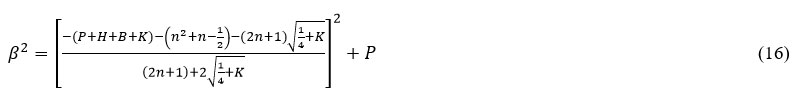
The above equation can be solved explicitly and the energyeigen spectrum of the Klein-Gordon equation with MHHP becomes
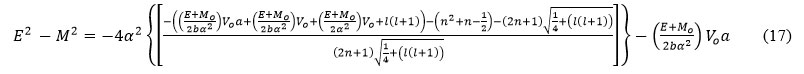
Solutions of the Schrodinger equation
The l-State Schrodinger Equation [27] with vector V(r), potential is given as
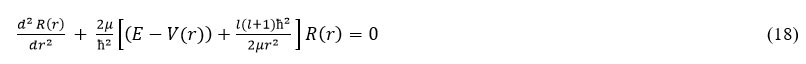
Where E, V(r), µ and I
are the energy, potential, reduced mass and angular momentum respectively Substitute eqn. (11) into eqn. (18) we have
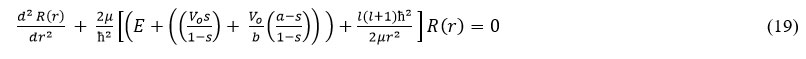

Similarly, using equations (6), (21) and (22) we obtain the energyeigen spectrum of the newly proposed interacting potential (MHHP) for Schrodinger equation given as:
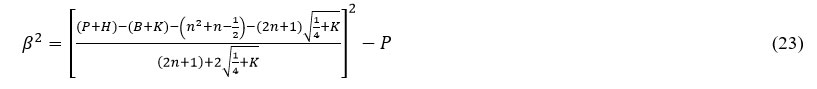
The above equation can be solved explicitly and the energyeigen spectrum of Schrodinger equation with MHHP becomes

We then obtain the radial wave function from the equation

Where n is a positive integer and Nn is the normalization constant
Discussions
In this section, we are going to consider certain case of potential evaluation to enable check the behavior of the obtained bound state solutions:
When Vo = 0, eqn. (24) is reduced to l-state solution of the Schrodinger equation with no potential interaction:

Similarly, eqn (17) is also reduced to l-state solution of the Klein-Gordon equation in the absence of interacting potential
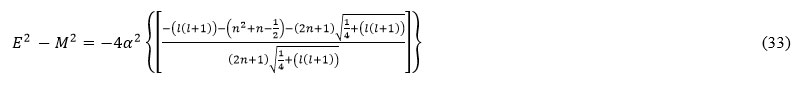
Acknowledgment
We thank our colleagues’ in Mathematics Department, University of Calabar, for their painstaking scientific input leading to the success of this our research work! The author is deeply grateful for the financial support of each co-authors leading to the success of this manuscript!
Conclusions
In this paper, we solved explicitly the Klein-Gordon and Schrodinger equations for the modified Hylleraas plus Hulthen potential for arbitrary states by using the parametric form of the Nikiforov-Uvarov method. By using the Pekeris-type approximation for the centrifugal term, we obtained approximately the energy eigenvalues and the unnormalized wave function expressed in terms of the Jacobi polynomials for arbitrary wave states. It is hope that the results we obtained in this research work could enlarge and enhance the application of the Hylleraas-Hulthen potentials (which is our newly proposed potentials) in the relevant fields of physics and atomic spectroscopy.
Reference
- S. M. Ikhdair and R. Sever, “A perturbative treatment for the bound states of the Hellmann potential,” Journal of Molecular Structure: THEOCHEM. 2007;809(1–3):103–113.
- R. Sever, C. Tezcan, Ö. Yesiltas, and M. Bucurgat, “Exact solution of effective mass Schrödinger equation for the hulthen potential,” International Journal of Theoretical Physics. 2008;47(9):2243–2248.
- I. B. Okon, E. E. Ituen, O. O. Popoola, and A. D. Antia, “Analytical solutions of Schrodinger equation with Mie-type potential using factorisation method,” International Journal of Recent Advances in Physics. 2013;2(2):1–7.
- G. Chen, “Bound states for Dirac equation with Wood-Saxon potential,” Acta Physica Sinica. 2004;53(3):680–683.
- V. M. Villalba and C. Rojas, “Bound states of the Klein-Gordon equation in the presence of short range potentials,” International Journal of Modern Physics A. 2006;21(2):313–325.
- I. B. Okon, O. O. Popoola, and E. E. Ituen, “Bound state solution to Schrodinger equation with Hulthen plus exponential Coulombic potential with centrifugal potential barrier using parametric Nikiforov-Uvarov method,” International Journal of Recent Advances in Physics. 2016;5(2).
- G. Chen, Z.-D. Chen, and Z.-M. Lou, “Exact bound state solutions of the s-wave Klein-Gordon equation with the generalized Hulthen potential,” Physics Letters. A. 2004;331(6):374–377.
- V. H. Badalov, H. I. Ahmadov, and S. V. Badalov, “Any l-state analytical solutions of the Klein-Gordon equation for the Woods-Saxon potential,” International Journal of Modern Physics E. 2010;19(7):1463–1475.
- A. Arda and R. Sever, “Approximate â„“-state solutions of a spin-0 particle for Woods-Saxon potential,” International Journal of Modern Physics C. 2009;20(4):651–665.
- S.-H. Dong, Factorization Method in Quantum Mechanics, vol. 150 of Fundamental Theories of Physics, Springer, Berlin, Germany, 2007.
- C. Berkdemir, A. S. Berkdemir, and R. Sever, “Systematical approach to the exact solution of the Dirac equation for a deformed form of the Woods-Saxon potential,” Journal of Physics. A. Mathematical and General. 2006;39(43):13455–13463.
- R. Dutt, K. Chowdhury, and Y. P. Varshni, “An improved calculation for screened Coulomb potentials in Rayleigh-Schrodinger perturbation theory,” Journal of Physics A: Mathematical and General. 1985;18(9)1379–1388.
- S. M. Ikhdair and R. Sever, “An alternative simple solution of the sextic anharmonic oscillator and perturbed coulomb problems,” International Journal of Modern Physics C. 2007;18(10)1571–1581.
- K. J. Oyewumi, F. O. Akinpelu, and A. D. Agboola, “Exactly complete solutions of the pseudoharmonic potential in N-dimensions,” International Journal of Theoretical Physics. 2008;47(4):1039–1057.
- H. Hassanabadi, S. Zarrinkamar, and A. A. Rajabi, “Exact solutions of D-dimensional Schrödinger equation for an energy-dependent potential by NU method,” Communications in Theoretical Physics. 2011;55(4):541–544.
- A. N. Ikot, A. D. Antia, L. E. Akpabio, and A. J. Obu, “Analytic solutions of Schrodinger equation with two-dimensional harmonic potential in cartesian and polar coordinates via Nikiforov-Uvarov method,” Journal of Vectorial Relativity. 2011;6(2):65–76.
- I. B. Okon, C. N. Isonguyo, E. E. Ituen, and A. N. Ikot, “Energy spectrum for some diatomic molecules with generalized manning-rosen potential using supersymmetric quantum mechanics (SUSY),” in Proceedings of the Nigerian Institute of Physics. 2014.
- I. B. Okon, O. Popoola, and C. N. Isonguyo, “Exact bound state solution of q-deformed woods-saxon plus modified coulomb potential using conventional Nikiforov-Uvarov method,” International Journal of Recent advances in Physics. 2014;3(4):29–38.
- I. B. Okon and O. O. Popoola, “Bound state solution of Schrodinger equation with Hulthen plus generalised exponential Coulomb potential using Nikiforov-Uvarov method,” International Journal of Recent Advances in Physics. 2015;4(3).
- C. N. Isonguyo, I. B. Okon, and A. N. Ikot, “Semi-relativistic treatment of Hellmann potential using Supersymmetric Quantum Mechanics,” Journal of the Nigerian Association of Mathematical Physics. 25(2):121–126.
- C. N. Isonguyo, I. B. Okon, A. N. Ikot, and H. Hassanabadi, “Solution of klein gordon equation for some diatomic molecules with new generalized morse-like potential using SUSYQM,” Bulletin of the Korean Chemical Society. 2014;35(12):3443–3446.
- R. L. Greene and C. Aldrich, “Variational wave functions for a screened Coulomb potential,” Physical Review A. 1976;14(6):2363–2366.
- P. K. Bera, “The exact solutions for the interaction V(r) = αr 2d-2 - βr d-2 by nikiforov-uvarov method,” Pramana—Journal of Physics. 2012;78(5):667–677.
- S. M. Ikhdair and R. Sever, “Relativistic and nonrelativistic bound states of the isotonic oscillator by Nikiforov-Uvarov method,” Journal of Mathematical Physics. 2011;52(12):Article ID 122108.
- Louis H., Ita B.I., Amos P.I., Akakuru O.U., Orosun M.M., Nzeata-Ibe N.A And Philip M Analytic Spin and Pseudospin Solutions to the Dirac Equation for the Manning-Rosen Plus Eckart Potential and Yukawa-Like Tensor Interaction IJCPS. 2018;7(1).
- H. Louis*, A. I. Ikeuba, B. I. Ita, P. I. Amos*, T. O. Magu, O. U. Akakuru and N. A. Nzeata1Energy Spectrum of the K-State Solutions of the Dirac Equation for Modified Eckart Plus Inverse Square Potential Model in the Presence of Spin and Pseudo-Spin Symmetry within the Framework of Nikifarov-Uvarov Method PSIJ. 2018;17(4):1-8; Article no.PSIJ.38209s
- Ita, B.I., Louis, H., Akakuru, O.U., Magu, T.O., Joseph, I.,Tchoua, P., Amos, P.I., Effiong, I. andNzeata, N.A. Bound State Solutions of the Schrodinger Equation for the More General Exponential Screened Coulomb Potential Plus Yukawa (MGESCY) Potential using Nikiforov-Uvarov Method. Journal of Quantum Information Science. 2018;8:24-45.
- Hitler L, Iserom IB, Tchoua P, Ettah AA. Bound State Solutions of the Klein-Gordon Equation for the More General Exponential Screened Coulomb Potential Plus Yukawa (MGESCY) Potential Using Nikiforov-Uvarov Method. J Phys Math. 2018;9:261.
- Louis H, Ita B.I., Amos P.I., Akakuru O.U., Orosun M.M., Nzeata-Ibe N.A And Philip M Bound State Solutions of Klein-Gordon Equation with Manning-Rosen Plus a Class of Yukawa Potential Using Pekeris-Like Approximation of the Coulomb Term and Parametric Nikiforov-Uvarov IJCPS. 2018;7(1).
- Louis Hitler, Benedict Iserom Ita, Pigweh Amos Isa, Nzeata-Ibe Nelson, Innocent Joseph, Opara Ivan, Thomas Odey Magu. Wkb Solutions for Inversely Quadratic Yukawa plus Inversely Quadratic Hellmann Potential. World Journal of Applied Physics. 2017;2(4):109-112. doi: 10.11648/j.wjap.20170204.13.
- Louis Hitler, Benedict Iserom Ita, Pigweh Amos Isa, Innocent Joseph, Nzeata-Ibe Nelson, Thomas Odey Magu, Opara Ivan. Analytic Spin and Pseudospin Solutions to the Dirac Equation for the Manning-Rosen Plus Hellmann Potential and Yukawa-Like Tensor Interaction. World Journal of Applied Physics. 2017;2(4)101-108. doi: 10.11648/j.wjap.20170204.12
- Akpan N.Ikot1, E. Maghsoodi , Oladunjoye A. Awoga, S. Zarrinkamar and H. Hassanabadi,Solution of Dirac Equation with Modified Hylleraas Potential under Spin and Pseudospin Symmetry Quant. Phys. Lett. 2014;3(1):7-14
- Serrano, F. A., Xiao-Yan Gu, and Shi-Hai Dong. "Qiang–Dong proper quantization rule and its applications to exactly solvable quantum systems." Journal of Mathematical Physics. 2010;51(8): 082103.

This work is licensed under a Creative Commons Attribution 4.0 International License.




