A Review on Invariant Manifolds and Targeted Energy Transfer
Maaita Jamal Odysseas1*  and Meletlidou Efthymia1
and Meletlidou Efthymia1
1Physics Department, Aristotle University of Thessaloniki, Greece .
Corresponding author Email: jmaay@physics.auth.gr
DOI: http://dx.doi.org/10.13005/OJPS03.02.02
We present a review on one of the latest developments in the field of dynamical systems, The nonlinear Targeted Energy Transfer (TET). The great significance of the phenomenon lies in the fact that the systems in which Nonlinear TET occurs present a form of self-tuning and can transfer energy over a wide variety of frequencies (resonances). This makes nonlinear TET particularly suitable in practical applications where it is necessary to extract energy from multiple ways of oscillation. Dynamical systems where nonlinear TET occurs are systems with different time scales and are singular. This property allows us to study such systems with the use of singular perturbation theory. It has been shown that Nonlinear TET is related to the bifurcation of the Slow Invariant Manifold of such systems and their slow flow.
Copy the following to cite this article:
Maaita Jamal Odysseas M. J, Efthymia M. A review on Invariant Manifolds and Targeted Energy Transfer. Orient J Phys Sciences 2018;2(2). 2018;3(2).
DOI:http://dx.doi.org/10.13005/OJPS03.02.02Copy the following to cite this URL:
Maaita Jamal Odysseas M. J, Efthymia M. A review on Invariant Manifolds and Targeted Energy Transfer 2017;3(2). Available from: https://bit.ly/3pWzZlR
Download article (pdf) Citation Manager Publish History
Select type of program for download
| Endnote EndNote format (Mac & Win) | |
| Reference Manager Ris format (Win only) | |
| Procite Ris format (Win only) | |
| Medlars Format | |
| RefWorks Format RefWorks format (Mac & Win) | |
| BibTex Format BibTex format (Mac & Win) |
Article Publishing History
| Received: | 08-06-2018 |
|---|---|
| Accepted: | 18-10-2018 |
Introduction
Systems that evolve depending on time are called Dynamical System. Such systems can be seen in many different scientific fields as mechanics and oscillations, biology, economy and others.1
Dynamical systems were introduced in Newton’s laws. Especially, by Newton’s second law that states that the rate of change of momentum of a body is directly proportional to the force applied and in its direction.
Since then a huge work has been done by several scientists. It isPoincare’s work on celestial mechanics, his theorems and methods,Lyapunov’swork on stability. It is the work ofAndronov and the USSR group at Gorki together with Pontryagin, Vitt and Khaiken on structural stability and nonlinear oscillations. It is the work of Kolmogorov, Anosov, Arnold and Sinai on ergodic theory,Birkhoff’swork on homoclinic point of a two-dimensional map. Also, it is the work on van der Pol equation by several scientists as Levinson, Smale’s work on the topological approach of studying dynamical systems and many others.6
The detection of deterministic chaos24 firstly by Poincaré and then, with the help of computers, by Lorenz opened a new era in the field of dynamical systems.
Chaos theory gave us a new perspective on approaching and understanding physical reality. A new window in understanding complex systems and behaviors was opened.
Dynamical systems and chaos concerns mainly nonlinear systems of differential equations and nonlinear mappings and is a vital subject of Applied Mathematics. The authors usually use first order differential equations since there exist theorems that guarantee the existence and uniqueness of solutions of these equations.
Dynamical systems are a field of applied mathematics and physics that is still developing. In this review article we present one of the latest developments in the field of dynamical systems: The nonlinear Targeted Energy Transfer(TET).21
Nonlinear TET phenomenon has been extensively studied the last 20 years and many applications have been introduced. The great significance of the phenomenon lies in the fact that the systems in which nonlinear TET occurs present a form of self-tuning and can transfer energy over a wide variety of frequencies (resonances). This makes Nonlinear TET particularly suitable in practical applications where we need energy to be extracted from multiple ways of oscillation.
Dynamical systems where nonlinear TET occurs are systems with different time scales and are singular. This property allows us to study such systems with the use of singular perturbation theory. It has been shown that nonlinear TET is related to the bifurcation of the Slow Invariant Manifold of such systems and their slow flow.
In the second section of this review article we present TET. We define the phenomenon, show its properties, its applications and some recent developments. In the third section we present basic theory of Invariant Manifolds and Singular Perturbation Theory. In the fourth section we highlight the relation between Nonlinear Energy Transfer Phenomenon, the bifurcations of Slow Invariant Manifolds and the behavior of the slow flow of such systems. Finally, we conclude in the fifth section.
Targeted Energy Transfer (TET)
The one way directed energy transfer from an initial system (donor) to a final system (receptor) is called Targeted Energy Transfer (TET). This procedure plays an important role in many physical phenomena. In biology, it plays a role in the process of energy transfer during the photosynthesis, in the proteins and DNA, In dynamics, on systems of nonlinear oscillators and breathers. In materials, on applications of superconductivity etc.
An important application of TET is the development of reliable and efficient energy harvesting devices which can collect energy from various external sources and make use of it. Such examples have been studied on mechanical systems that convert external oscillations into useful electrical energy.21
The main mechanism behind the TET is the resonances between the donor and the receptor. Particularly, in the case of a single mode energy attractors the energy transfer occurs in a restricted band of frequencies that are related with the given frequency of the system.
There is great importance in mechanical systems attached to local attachment possessing essential stiffness nonlinearity. The addition of such nonlinear attachments to the linear systems significantly affect the overall dynamical behavior. This happens due to the lack of preferential resonance frequency of the nonlinear attachment and leads it to have resonances over a broad frequency range.
This property of the local attachment with essential stiffness nonlinearity gives the ability to use such attachments as a Nonlinear Energy Sinks (NESs). Indeed, under certain initial conditions a one- way, irreversible (on the average) flow of the energy from the linear to the nonlinear attachment occurs. This phenomenon is called nonlinear TET.
The NES may participate in a set of transitive nonlinear resonances. Depending on the instantaneous energy level the NES transitionally tunes, for a finite time, and exports energy. Then “escapes” from this resonance because of energy dissipation and participates in another transitional tune with a different frequency level. The control parameter of this procedure is the instantaneous energy level of the system.
The NES can be adjusted in a way that it will firstly extract energy from rich energy states and then tuned in a way to extract energy from states with less energy. This makes it particularly suitable in practical applications where it is necessary to extract energy from multiple ways of oscillation.
The cause of this behavior of the NES lies in the fact that the addition of essential nonlinear attachment to the linear system introduces high degeneracy in the dynamics of the system and give the ability for large bifurcations and complex dynamical phenomena.
Gendelman at 20015 was the first to observe and study the nonlinear TET. He studied the transient dynamics of a system of two degrees of freedom consists of a linear oscillator with damping coupled weakly with an essential nonlinear oscillator. On this system, he observed that for certain initial conditions of energy given in the linear oscillator (above a threshold) there was a TET to the nonlinear oscillator which absorbed most of the energy. More extensive study of the above phenomenon4,20 proved that the basic mechanism that controls TET was the 1:1 transitional resonance between the linear and the nonlinear system. Also proved that the existence of dissipation is a prerequisite for TET, whereas, in the absence of damping beating phenomena are occurred, i.e. the energy is transferred from the linear to the nonlinear and back again to the linear oscillator.
The first experimental demonstration of a TET in a mechanical system took place in 2005 by McFarland, Bergman and Vakakis,15 where they studied a system consists of two, one linear and one nonlinear, one degree of freedom, oscillators with a stiff linear coupling and a dissipative NES. With the above experiment, the researchers noticed good theoretical and experimental agreement despite the strong nonlinearity and the transient nature of the dynamics of the problem. Indeed, the energy which was introduced in the linear oscillator transferred to the NES where it was locally dissipated. The results of the above experiment confirmed the existence of an energy threshold after which starts the phenomenon of TET.
The initial energy of the system (the amplitude of the oscillation) plays an essential role on the TET phenomenon. This fact is related to the mechanisms of energy transfer. Certain criteria that relates the initial energy (amplitude) with the TET have configured in different papers.19
An Illustrative Example: Let consider a system consists of a nonlinear y1 (t) oscillator coupled to a linear y2 (t)
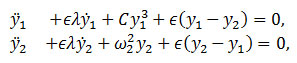
where λ is the damping parameter, ω2 the frequency of the linear oscillator and C the nonlinear coefficient. The Hamiltonian of this system is
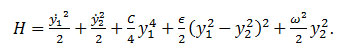
The instant energy of the nonlinear oscillator is given by
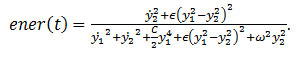
Considering zero initial displacements for both oscillators and zero velocity for the nonlinear oscillator and solve numerically the system of the differential equations for different values of the initial velocity Y of the linear oscillator and small values of the damping parameter we get the following results.
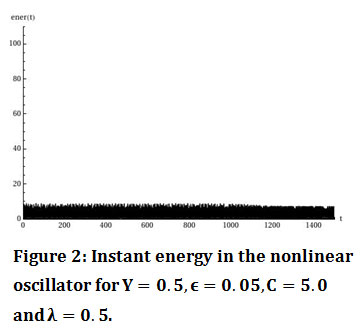
For initial value Y=0.5, for the parameters: λ=0.5,ω_2^2=0.9,C=5,ϵ=0.05 the oscillations y_1 (t),y_2 (t) are given by figure 1. From the diagram of the instant energy on the nonlinear oscillator (figure 2) we conclude that there is no energy transfer between the two oscillators.
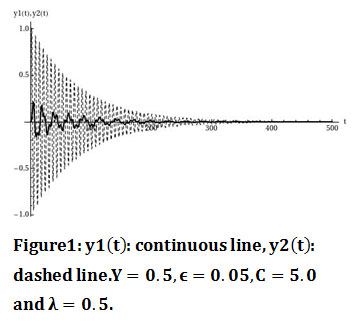 |
Figure 1: y1(t): continuous line, y2(t): dashed line.Y=0.5,ϵ=0.05,C=5.0 and λ=0.5. |
|
|
Figure 2: Instant energy in the nonlinear oscillator for Y=0.5,ϵ=0.05,C=5.0 and λ=0.5. |
The system continues to oscillate without having energy transfer from the linear to the nonlinear oscillator until the initial velocity takes the value Y=1.71. For this initial velocity the system oscillates in a way as it is shown in figure 3. Figure 4 shows that for this value of the initial velocity energy transfer between the two oscillators occurs.
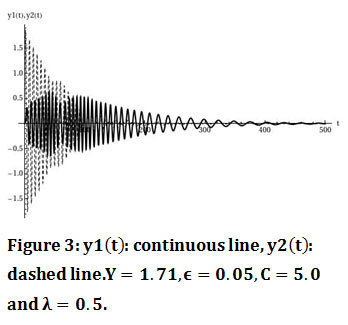 |
Figure 3: y1(t): continuous line, y2(t): dashed line.Y=1.71,ϵ=0.05,C=5.0 and λ=0.5. |
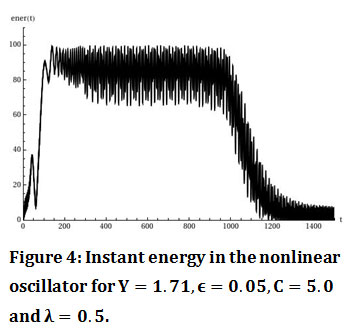 |
Figure 4: Instant energy in the nonlinear oscillator for Y=1.71,ϵ=0.05,C=5.0 and λ=0.5. |
For the initial value Y=5.0 the oscillations y_1 (t),y_2 (t) are given by figure 5. The diagram of the instant energy in the nonlinear oscillator (figure 6) shows that the energy of the system is transferred in the nonlinear oscillator in a one direction way so there is TET from the linear to the nonlinear oscillator. The procedure of the energy transfer starts for time t=160. The comparison between the oscillations y_1 (t),y_2 (t) (figure 7) shows that the oscillations between the oscillators are in 1:1 resonance.
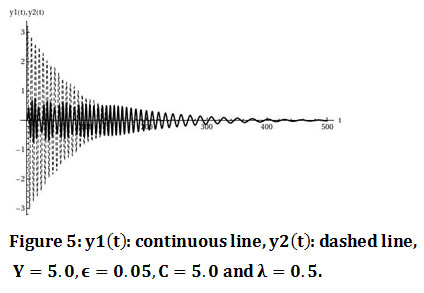 |
Figure 5: y1(t): continuous line, y2(t): dashed line, Y=5.0,ϵ=0.05,C=5.0 and λ=0.5. |
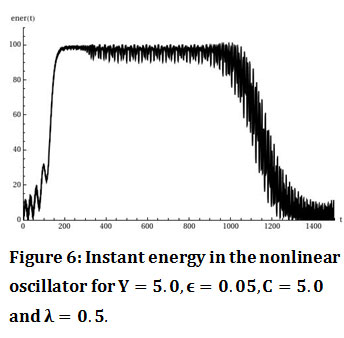 |
Figure 6: Instant energy in the nonlinear oscillator for Y=5.0,ϵ=0.05,C=5.0 and λ=0.5. |
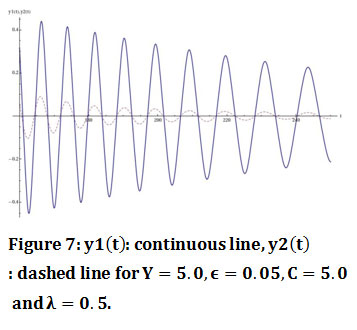 |
Figure 7: y1(t): continuous line, y2(t): dashed line for Y=5.0,ϵ=0.05,C=5.0 and λ=0.5. |
The above example shows that the phenomenon of the TET is related to systems initial energy. Moreover, TET occurs when there is a 1:1 resonance between the two oscillators. The conclusion from the above remarks is that to have TET the amount of energy that is given in the system must be enough to lead the system to a transient 1:1 resonance.
The phenomenon of TET may be interpreted by three mechanisms. The first mechanism is the basic (1:1) resonance between the donor and the receptor that leads to the basic TET. The second mechanism is the subharmonic resonance that leads to the subharmonic TET. The third mechanism is based on the excitation of the so-called impulsive periodic or semi-periodic orbits which leads through rhythmic phenomena to one of the previous two mechanisms.
TET occurs even in the case where the NES is attached to a system with external excitations. In this case the system, in addition to the known steady state oscillations with the weak variation of the responses, perform very special oscillations with large variations of the responses which are called Strongly Modulated Responses. These responses can be considered as the extension of the phenomenon of TET in systems with external excitations since the Strongly Modulated Responses can be considered as a form of iterative TET.
Applications of TET between linear and nonlinear oscillators have great interest.
In recent years, intense efforts have been done in this area. Papers have been published concerning seismic mitigation of energy in buildings and the use of the TET phenomenon to transfer and dissipate the energy to protect the buildings.
For example, Nucera et al.,16 report experimental validation of using nonlinear targeted energy transfers for seismic mitigation by experiments with a three- story shear-frame structure under seismic excitation in the form of two different historic earthquakes. The experimental design consists of either a single nonlinear energy sink or a combination of two nonlinear energy sinks attached at floors of the test structure. The researchers show that the combination of two NESs an NES with smooth stiffness nonlinearity at the top floor and a vibro- impact NES at the bottom floor of the test structure lead to dramatic reduction of the structural seismic response.
Tripepi et al.,18 show that TET can be applied to protect seismically excited eccentric steel structures. They considered a small-scale four-story unsymmetrical- plan building, modeled as a twelve-degree-of- freedom-system. The floors were sufficiently rigid so that the frame can reasonably be considered as shear-type. Each floor has an additional eccentric mass and two NESs were placed on the top of it. They showed that the nonlinear attachments can engage in transient resonance with linear modes at arbitrary frequencies by generating TET of vibration from the primary structure to local attachment.
There are studies on application of the TET to stabilize drill-string systems. Viguie et al.,22 use a nonlinear Energy Sink to absorb the unwanted vibrational energy from a drill system.
Furthermore, there are studies on transferring of unused energy in automotive gearboxes systems8 or for modal energy redistribution in automotive drivetrains. Motato et al.,14 used TET to mitigate the broadband torsional oscillations generated by compact high output power-to-weight ratio internal combustion engines and transmitted to lightly damped drivetrain systems.
The study of TET has not stopped. New phenomena, applications and implementations are published in several papers.
For example, Farid et al., 3 presented numeric evidence for the efficiency of the applicability of common pendulum as the NES for mitigation of impulsive excitations. They discussed that the pendulum NES can overcome one of the main shortcomings of more traditional NES designs, since it is able to mitigate excitation of a primary system in a relatively wide range of initial energies, because it can be captured into a resonance with primary oscillator both for rotational and oscillatory responses.
Saeed et al., 17 employed a novel rotating and vibro-impact NESs for rapid and passive TET.
Dekemele et al., 2 performed measures for the speed of both Targeted Energy Transfer and Resonance Capture Cascading and introduced the pumping time and the cascading time, respectively.
Invariant Manifolds
A powerful tool for analyzing high-dimensional singular systems is the Geometric Singular Perturbation Theory.7,23
A map f:X→Y of subsets of two Euclidean spaces is called C^r diffeomorphism if it is one to one and onto and if the inverse map f^(-1):Y→X is also C^r.
A subset M⊂R^n is called a C^r manifold of dimension m if:
There exists a countable collection of open sets V^a⊂R^n, a∈A, where A is some countable index set, with U^a≡V^aâ‹‚M such that M=∪_(a∈A) U^α.
There exist a C^r diffeomorphism x^a defined on each U^a which maps U^a onto some open set in R^m.
The change of the coordinates in the overlapping region of two of the open sets U^a must also be C^r.
A manifold contained in the phase space of a dynamical system which has the property that its orbits remain on the manifold throughout the course of their dynamical evolution is called Invariant Manifold.
We consider the equations of the form
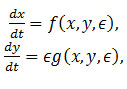
where x∈R^n, y∈R^l, ϵ is a real parameter, f,g are C^∞ on a set U×I, where U⊂R^(n+l) and I is an open interval containing 0.With a change of time-scale, considering the slow time τ=ϵt, system (4) becomes
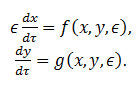
System (4) is called fast and (5) is called slow system. Let assume an l-dimensional manifold, possibly with boundary, M_0 which is contained in the set {f(x,y,0)=0} and the fundamental hypothesis on M_0 that as a set of critical points, the directions normal to the manifold will correspond to eigenvalues that are not neutral. The manifold M_0 is said to be normally hyperbolic if the linearization of (4) at each point in M_0 has exactly l eigenvalues on the imaginary axis Re(λ)=0. A set M is locally invariant under the flow form (4) if it has a neighborhood V so that no trajectory can leave M without also leaving V.
In what follows we present a set of theorems that play important role in the geometric singular perturbation theorem.
Fenichel’s Invariant Manifold Theorem I
If ϵ>0 but sufficiently small, there exists a manifold M_ϵ that lies within O(ϵ) of M_0 and is diffeomorphic to M_0. Moreover, it is locally invariant under the flow of system (4), and C^r, including in ϵ, for any r<+∞.
The manifold M_ϵ is called the slow manifold and it is locally invariant.
Fenichel’s Invariant Manifold Theorem II
If ϵ>0, but sufficiently small, there exists stable manifolds W^s (M_ϵ ) and unstable manifolds W^u (M_ϵ ) that lie within O(ϵ) of, and are diffeomorphic to, the stable manifold W^s (M_0 ) and to the unstable manifold W^u (M_0 ) respectively. Moreover, they are each locally invariant under (4), and C^r, including in ϵ, for any r<+∞.
Tikhonov Theorem: Consider the initial value problem
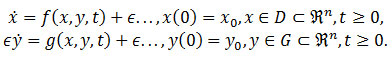
For f and g, we take sufficiently smooth vector functions in x,y and t. We assume that a unique solution of the initial value problem exists and suppose this holds also for the reduced problem 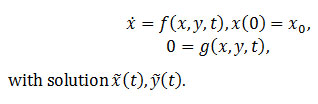
Suppose that 0=g(x,y,t) is solved by y ̃=Φ(x,t), where Φ(x,t) is a continuous function and an isolated root. Also, suppose that y ̃=Φ(x,t) is an asymptotically stable solution of the equation dy/dτ=g(x,y,t) that is uniform in the parameters x∈D and t∈R^+. y(0) is contained in an interior subset of the domain of attraction of y ̃=Φ(x,t) in the case of the parameter values x=x(0),t=0. Then, we have
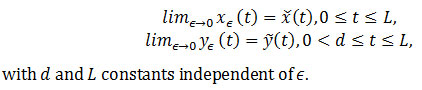
The relation between slow flow, Invariant Manifolds and TET
Dynamical systems where TET occurs are singular because the mass of the NES is much smaller in comparison to the linear system.
As a result, Singular Perturbation Theory and Invariant Manifolds are important mathematical tools that help us study systems with TET.
The first to make such studies was Gendelman 5 who showed that the rate of the dissipation of the energy is connected to the bifurcations of the invariant manifold.
In his work showed that the presence of bifurcations of the invariant manifold has rather essential effect on the dynamics of the system. Namely, passage through the bifurcation can destroy the regime of nonlinear normal mode and facilitate the energy dissipation. So, the damping coefficient should be chosen to ensure the possibility for bifurcations of the Nonlinear Normal Modes invariant manifold. Failure to do so will result in a loss of NES ability to dissipate the energy of vibrations.
Maaita et al., 9-11 studied an autonomous damped system of three degrees of freedom, composed of two linear coupled oscillators with an essentially nonlinear lightweight attachment
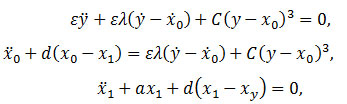
where a,d,C,λ and ϵ≪1 are the parameters of the system. With the help of system reduction and the use of Complexification- Averaging Technique13 they derived the Slow Invariant Manifold (SIM) and the slow flow of the system and showed that they effect on the dynamics of the system.
In 9 they showed that the SIM of the above system provides information about the asymptotic behavior of the orbits of the system. Specifically, the SIM of the system may have one or three branches depending on the slow time and the value of the damping parameter (figure 8). The corresponding bifurcations affect the dynamical behavior of the system which can change drastically. Indeed, Tikhonov’s theorem guarantees that, when the branches of the SIM are isolated and stable, the orbits of the system tend to these stable branches as long as they exist. Also, Fenichel’s theorems guarantee that the unstable branch of the SIM will have stable and unstable manifolds that will generically intersect transversally and lead to chaotic behavior.
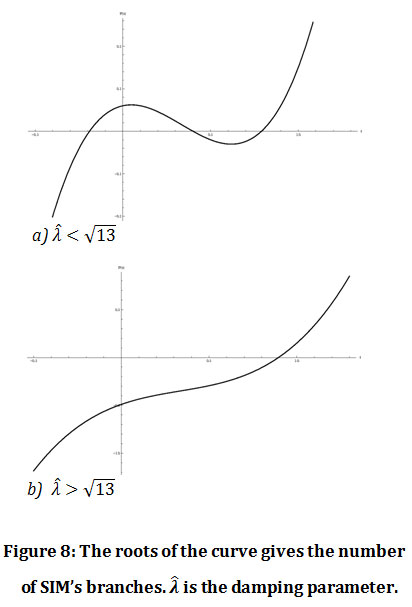 |
Figure 8: The roots of the curve gives the number of SIM’s branches. λ is the damping parameter. |
Furthermore, the damping parameter and the number of the branches of the SIM play an essential role in the evolution of the dynamics of the system. The dynamics can be simple, as in the case where there is only one persisting stable branch of the SIM, or complicated, when bifurcations of the SIM occur, resulting in different phenomena such as relaxation oscillations, orbit excitations (figure 9) and complex structures of the basins of attraction, especially when the damping parameter is small.
In [10] they studied the dynamics of the slow flow of the system. The dynamics of the Slow flow and the structure of the SIM are connected. There are cases when the slow flow oscillates near the region of the SIM regularly and is attracted to a periodic orbit. When the SIM has saddle node bifurcations the slow flow has relaxation oscillation (i.e. the system oscillates regularly around one branch of the SIM and suddenly jumps to the other branch). It is interesting to note that when we have bifurcations of the SIM, in one hand, the system may have regular behavior and in the other hand, for different values of the parameters, may have chaotic behavior and therefore the slow flow becomes unpredictable (figures 10).
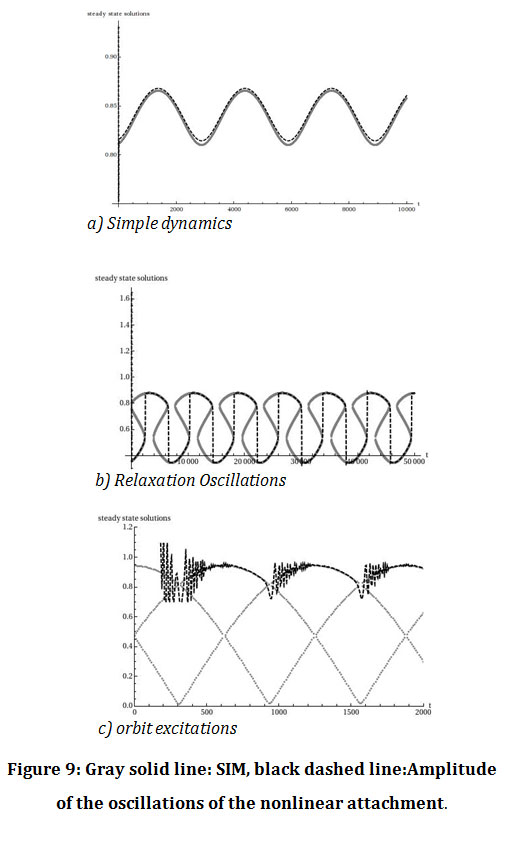 |
Figure 9: Gray solid line: SIM, black dashed line: Amplitude of the oscillations of the nonlinear attachment. |
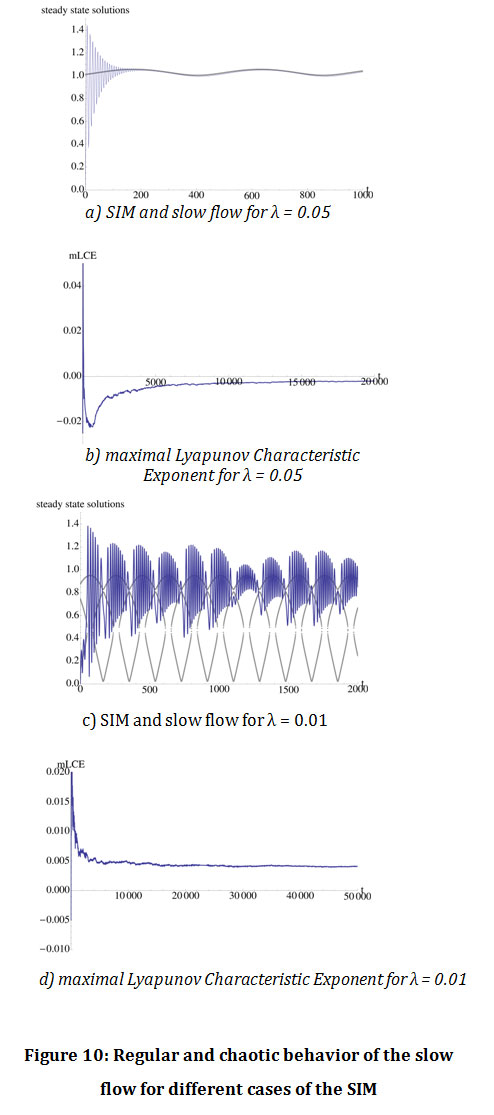 |
Figure 10: Regular and chaotic behavior of the slow flow for different cases of the SIM |
The relation between slow flow dynamics, the structure of the SIM and the energy transfer from the linear to the nonlinear oscillator has been investigated in.11 There, they concluded that the bifurcations of the SIM and the dynamics of the slow flow play an important role in the energy transfer from the linear to the nonlinear oscillator and the dissipation of the total energy of the initial system.
When the SIM has no bifurcations, there is no energy transfer from the linear to the nonlinear oscillator and the energy dissipates smoothly (figure 11). When the SIM has bifurcations, then energy transfer occurs. Furthermore, when there is energy transfer to the nonlinear oscillator, the rate of the dissipation of the total energy of the system becomes larger (figure 12).
When the slow flow oscillates rapidly around the SIM, the energy is transferred to the nonlinear oscillator (figures 13). The amount of energy that transfers is related to the initial energy given to the system.
An important result is derived in12 where it has been proved that the SIM of systems as (6) may bifurcate only if the order of the nonlinear oscillator is an odd number, that is, k=2n+1, where n=1,2,....
Thus, we conclude that to have TET between the linear oscillators and the Nonlinear Oscillator that behaves as a Non-Energy Sink, the Non-Energy Sinks for systems as (6) must be nonlinear oscillators with odd order.
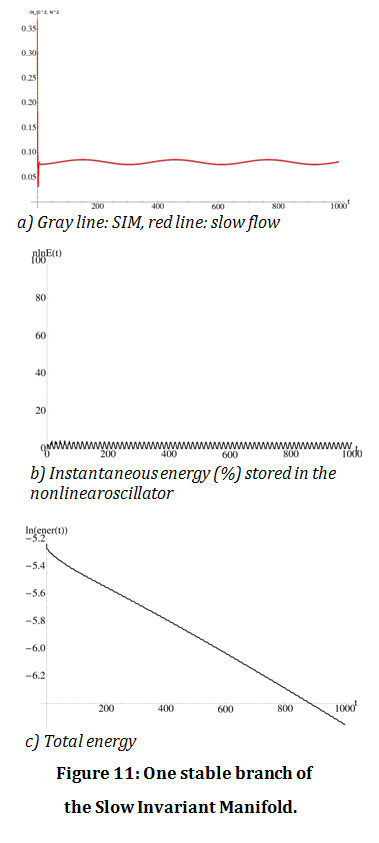 |
Figure 11: One stable branch of the Slow Invariant Manifold. |
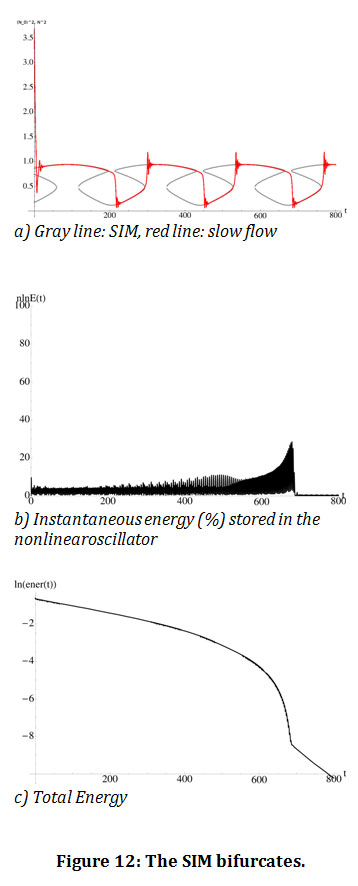 |
Figure 12: The SIM bifurcates. |
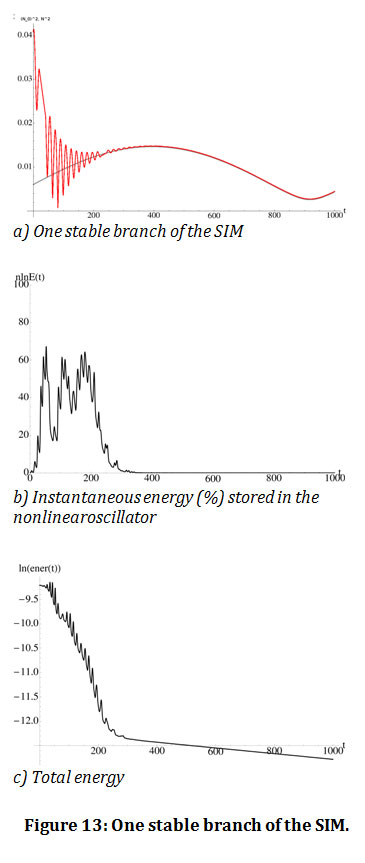 |
Figure 13: One stable branch of the SIM. |
Conclusions
Nonlinear TET is a phenomenon where energy may transfer between linear and nonlinear oscillators. This phenomenon can be very important in a wide variety of mechanical, electronic and other applications.
Such systems of coupled oscillators have the property that the nonlinear attachment has a small mass in comparison to the masses of the linear oscillators and therefore the problem is singular.
Singular perturbation theory, such as Fenichel’s and Tikhonov’s theorems, can be used to study systems where Nonlinear TET take place.
SIMs and the slow flow of such systems play important role on the dynamics of the systems and affect the energy transfer from the linear to the nonlinear oscillator and the rate of the total energy dissipation.
When the SIM has no bifurcations and the slow flow has regular orbits there is no energy transfer from the linear to the nonlinear oscillator.
In the contrary, Nonlinear Energy Transfer occurs when the SIM bifurcates, and the slow flow has a more complex oscillation.
Bifurcations of the SIM occurs where the nonlinear oscillator of the systems has an odd order nonlinearity.
References
- Arrowsmith D.K., Place C.M., An Introduction to Dynamical Systems, Cambridge University Press. 1994.
- Dekemele., Kevin., Robin De Keyser., Mia Loccufier. Performance measures for targeted energy transfer and resonance capture cascading in nonlinear energy sinks. Nonlinear Dynamics. 2018;1-26
- Farid., Maor., Oleg V. Gendelman. Tuned pendulum as nonlinear energy sink for broad energy range. Journal of Vibration and Control. 2017;23(3):373-388.
CrossRef - Gendelman O.V., Manevitch L.I., Vakakis A.F., M’Closkey R. Energy Pumping in Nonlinear Mechanical Oscillators: Part I- Dynamics of the Underlying Hamiltonian Systems, J. Appl. 2001;68:34-41.
CrossRef - Gendelman, O.V. Bifurcations of nonlinear normal modes of linear oscillator with strongly nonlinear damped attachment, Nonlinear Dynamics. 2004;37:115-128.
CrossRef - Hansen V. L., Gray J. eds. History of Mathematics. EOLSS Publications. 2010.
- Jones C.K.R.T. Geometric Singular Perturbation Theory, Dynamical Systems, Lecture Notes in Mathematics, Springer Verlag. 1995
- Karagiannis I., Theodossiades S. Targeted energy transfer in hypoid gears of automotive differentials, ENOC. 2011.
- Maaita J.O., Meletlidou E., Vakakis A.F., Rothos V. The effect of Slow Flow Dynamics on the Oscillations of a singular damped system with an essentially nonlinear attachment, Journal of Applied Nonlinear Dynamics. 2013;2(4):315-328.
CrossRef - Maaita J.O., Meletlidou E., Vakakis A. F., Rothos V. The dynamics of the slow flow of a singular damped nonlinear system and its Parametric Study, Journal of Applied Nonlinear Dynamics. 2014;3(1):37–49.
CrossRef - Maaita J.O., Meletlidou E. The Effect of Slow Invariant Manifold and Slow Flow Dynamics on the Energy Transfer and Dissipation of a Singular Damped System with an Essential Nonlinear Attachment, Journal of Nonlinear Dynamics Volume 2014, Article ID 208171, 10 pages. 2014.
- Maaita J.O. Theorem on the Bifurcations of the Slow Invariant Manifold of a System of Two Linear Oscillators Coupled to a k-order Nonlinear Oscillator, Journal of Applied Nonlinear Dynamics. 2016;5(2):193–197.
CrossRef - L. I. Manevitch. Complex representation of dynamics of coupled oscillators, in Mathematical Models of Nonlinear Excitations, Transfer Dynamics and Control in Condensed Systems, Kluwer Academic Publishers/Plenum, New York. 1999;269-300.
CrossRef - Motato., Eliot., Ahmed Haris., Stephanos Theodossiades., Mahdi Mohammadpour., Homer Rahnejat., P. Kelly., A. F. Vakakis., D. M. McFarland., L. A. Bergman. Targeted energy transfer and modal energy redistribution in automotive drivetrains. Nonlinear Dynamics. 2017;87(1):169-190.
CrossRef - McFarland D. M., Bergman L. A., Vakakis A. F. Experimental study of non-linear energy pumping occurring at a single fast frequency, Int. J. Nonlinear Mech. 2005;40:891-899.
CrossRef - Nucera F., Lo Iacono F., McFarland D.M., L. A. Bergman L. A., Vakakis A. F. Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: Experimental results, J. of Sound and Vibration. 2008;313:57-76.
CrossRef - Saeed., Adnan S., Mohammad A. AL-Shudeifat. A New Type of NES: Rotary Vibro-Impact, ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers. 2017.
- Tripepi, Concetta, et al., Application of Targeted Energy Transfer (TET) Techniques to the Seismic Protection of a Small Scale Multistory Eccentric Steel Structure, ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers. 2011.
- Vakakis A.F. Inducing Passive Nonlinear Energy Sinks in Vibrating Systems, J. Vib. Acoust. 2001;123:324-332.
CrossRef - Vakakis A. F., Gendelman O. V. Energy Pumping in Nonlinear Mechanical Oscillators: Part II- Resonance capture, J. Appl. Mech. 2001;68:34-41.
CrossRef - Vakakis A. F., Gendelman O. V., Bergman L. A., McFarland D. M., Kerschen G., Lee Y. S. Nonlinear Target Energy Transfer in Mechanical and Structural Systems, Springer Verlag. 2008.
- Viguie R., Kerschen G., Golinval J. C., McFarland D. M., Bergman L. A., Vakakis A. F., van de Wouw N. Using Targeted Energy Transfer to Stabilize Drill-string Systems, Mechanical Systems and SignalProcessing. 2009;23:148-169.
CrossRef - Wiggins S. Global Bifurcations and Chaos, Analytical Methods, Applied Mathematical Sciences, Springer Verlag.1988.
CrossRef

This work is licensed under a Creative Commons Attribution 4.0 International License.